Normal extension

In abstract algebra, an algebraic field extension L/K is said to be normal if L is the splitting field of a family of polynomials in K[X]. Bourbaki calls such an extension a quasi-Galois extension.

1 Equivalent properties and examples
2 Other properties
3 Normal closure
4 References
5 See also

Equivalent properties and examples

The normality of L/K is equivalent to each of the following properties:

Let K^a be an algebraic closure of K containing L. Every embedding σ of L in K^a which restricts to the identity on K, satisfies σ(L) = L. In other words, σ is an automorphism of L over K.
Every irreducible polynomial in K[X] which has a root in L factors into linear factors in L[X].
The minimal polynomial over K of every element in L splits over L.

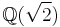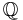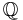For example, $\mathbb{Q}(\sqrt{2})$ is a normal extension of $\mathbb{Q}$ , since it is a splitting field of x² − 2. On the other hand, $\mathbb{Q}(\sqrt[3]{2})$ is not a normal extension of $\mathbb{Q}$ since the polynomial x³ − 2 has one root in it (namely, $\sqrt[3]{2}$ ), but not all of them (it does not have the non-real cubic roots of 2).

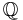The fact that $\mathbb{Q}(\sqrt[3]{2})$ is not a normal extension of $\mathbb{Q}$ can also be proved using the first of the two equivalent properties from above. The field 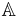$\mathbb{A}$ of complex algebraic numbers is an algebraic closure of 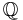$\mathbb{Q}$ containing $\mathbb{Q}(\sqrt[3]{2})$ . On the other hand

$\mathbb{Q}(\sqrt[3]{2})=\{a%2Bb\sqrt[3]{2}%2Bc\sqrt[3]{4}\in\mathbb{A}\,|\,a,b,c\in\mathbb{Q}\}$

and, if ω is one of the two non-real cubic roots of 2, then the map

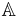$\begin{array}{rccc}\sigma:&\mathbb{Q}(\sqrt[3]{2})&\longrightarrow&\mathbb{A}\\&a%2Bb\sqrt[3]{2}%2Bc\sqrt[3]{4}&\mapsto&a%2Bb\omega%2Bc\omega^2\end{array}$

is an embedding of $\mathbb{Q}(\sqrt[3]{2})$ in $\mathbb{A}$ whose restriction to 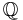$\mathbb{Q}$ is the identity. However, σ is not an automorphism of $\mathbb{Q}(\sqrt[3]{2})$ .

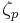For any prime p, the extension $\mathbb{Q}(\sqrt[p]{2}, \zeta_p)$ is normal of degree p(p − 1). It is a splitting field of x^p − 2. Here $\zeta_p$ denotes any pth primitive root of unity.

Other properties

Let L be an extension of a field K. Then:

If L is a normal extension of K and if E is an intermediate extension (i.e., L ⊃ E ⊃ K), then L is also a normal extension of E.

If E and F are normal extensions of K contained in L, then the compositum EF and E ∩ F are also normal extensions of K.

Normal closure

If K is a field and L is an algebraic extension of K, then there is some algebraic extension M of L such that M is a normal extension of K. Furthermore, up to isomorphism there is only one such extension which is minimal, i.e. such that the only subfield of M which contains L and which is a normal extension of K is M itself. This extension is called the normal closure of the extension L of K.

If L is a finite extension of K, then its normal closure is also a finite extension.

References

Lang, Serge (2002), Algebra, Graduate Texts in Mathematics, 211 (Revised third ed.), New York: Springer-Verlag, ISBN 978-0-387-95385-4, MR 1878556
Jacobson, Nathan (1989), Basic Algebra II (2nd ed.), W. H. Freeman, ISBN 0-716-71933-9

Normal extension

Contents

Equivalent properties and examples

Other properties

Normal closure

References

See also